MATLAB ÖZEL DERSİ ALMAK İÇİN TIKLAYIN.
Matlab’da Matris İşlemleri
Bu bölümde Matlab’da aşağıdaki matris işlemlerini sırasıyla göreceksiniz.
-
Matlab’da Matris Tanımlama
-
Matlab’da Bir Matrisin Elemanlarına Ulaşma
-
Matlab’da Bir Matrisin Alt Matrislerine ve Vektörlerine Ulaşma
-
Matlab’da Matrislerin Yeniden Şekillendirilmesi
-
Matlab’da Matrislerin Boyutunun Değiştirilmesi
-
Matlab’da Bir Matrise Satır veya Sütun Eklenmesi
-
Matlab’da Bir Matrisin Satır/Sütununun Silinmesi
-
Matlab’da Matrislerin Birleştirilmesi
Matlab’da Matris Tanımlama
Örnek (Matlab’da Matris Oluşturma)
Matlab’da
$latex
A = \begin{bmatrix}
15 & 2 & 4 \\
3 & 7 & 11 \\
1 & 2 & 9
\end{bmatrix}
$
şeklindeki bir matrisi oluşturmak için, Matlab komut satırından ve editöründen:
A = [15 2 4 ; 3 7 11 ; 1 2 9]
komutu girilir ve cevap olarak
A =
15 2 4
3 7 11
1 2 9
yanıtı alınır.
Yukarıdaki işlemde görüldüğü üzere yeni satıra geçmek için “;” ifadesi kullanılıyor.
“;” ifadesini (yeni satıra geç ifadesini) KULLANMADAN
Alternatif olarak ;
A = [15 2 4
3 7 11
1 2 9]
şeklinde de Matlab’da bir matris oluşturabiliri. “;” koymak yerine enter tuşuna basarak alt satıra geçeriz ve bir sonraki satırın elemanlarını gireriz. Ne zaman ki ” ] “ifadesi ile matrisi kapatıp enter tuşuna basarız, o zaman işlem tamamlanır ve
A =
15 2 4
3 7 11
1 2 9
cevabını olarız.
Örnek (Matris Oluşturma)
Matrisin elemanları kompleks sayı da alabilir. Örneğin;
$latex
B = \begin{bmatrix}
3 +6 i & 8 i \\
6 + 10 i & 14
\end{bmatrix}
$
şeklindeki bir matrisi Matlab’da
B = [3+6i 8i ; 6+10i 14]
şeklinde girebiliriz ve Matlab komut ekranında cevap olarak
B =
3.0000 + 6.0000i 8.0000i
6.0000 +10.0000i 14.0000
ifadesini alırız.
Matlab’da Bir Matrisin Elemanlarına Ulaşma
Matlab’da tanımladığımız / oluşturduğumuz matrisler Matlab workspace’inde saklanır ve orada görünür.
Çalışma anında Matlab Komut Ekranından matrislerin adını yazıp tamamını çağırabildiğimiz gibi sadece bir elemanını veya içerisindeki bir parçayı da çağırmak isteyebiliriz.
A isimli bir matrisin elemanlarını çağırmak için:
A (satir_indeksi ; sutun_indeksi)
şeklinde bir format kullanırız.
Örnek : (Matrisin elemanlarını çağırma)
$latex
A = \begin{bmatrix}
15 & 2 & 4 \\
3 & 7 & 11 \\
1 & 2 & 9
\end{bmatrix}
$
şeklinde bir matrisimiz olsun. Bunu:
A = [15 2 4 ; 3 7 11 ; 1 2 9];
şeklinde tanımlarız.
A matrisinin bir elemanınının değerini bir değişkene atamak istiyorsak aşağıdaki yolu izleriz.
a23 isimli değişkene A matrisinin 2. satır – 3. sütundaki elemanını atamak isteyelim.
a23 = A(2,3)
ifadesini girdiğimizde
(A’nın 2.satır ile 3.sütun elemanına ulaşır.)
a23 =
11
cevabına ulaşırız.
Matlab’da Bir Matrisin Alt Matrislerine ve Vektörlerine Ulaşma
Matlab’da çok karşılaşılan uygulamalardan birisi ise matrisin içinde alt matrislere ulaşma veya sadece bir satır / sütuna ulaşma durumudur.
Bu durumda, bütün durumlar için aşağıdaki yapıyı kullanacağız:
A (satir_bilgisi ; sutun_bilgisi)
Örnek : (Alt Matrislere Ulaşma)
$latex
A = \begin{bmatrix}
15 & 2 & 4 \\
3 & 7 & 11 \\
1 & 2 & 9
\end{bmatrix}
$
şeklinde bir matrisimiz olsun.
Bu Matlab’da aşağıdaki şeklide gireriz.
A = [15 2 4 ; 3 7 11 ; 1 2 9];
altmatris = A (1:2 , 2:3) → gösterimi ile ulaşılacak alt matris, A’ nın 1-2.aralığındaki satırları ile 2-3.aralığındaki sütunlarının kesişim bölgesidir
altmatris =
2 4
7 11
Örnek :
$latex
A = \begin{bmatrix}
15 & 2 & 4 \\
3 & 7 & 11 \\
1 & 2 & 9
\end{bmatrix}
$
A = [15 2 4 ; 3 7 11 ; 1 2 9];
>> altmatris = A(1:2 , :) → gösterimi ile ulaşılacak alt matris , A’ nın 1.-2. Aralığındaki satırları ile tüm sütunların kesişimidir.Yani 1. ve 2. Satırlardan oluşan matristir.
altmatris =
15 2 4
3 7 11
A(3 , 2:3) → gösterimi ile A matrisinin 3.satırındaki 2-3 aralığındaki sütunundaki elemanları veren bir vektördür.
: → tüm satır / sütun
end → son satır / sütun
Örnek :
A(: , end) → gösterimi bütün satırlarla, son sütünün kesişimini verecektir.Yani son sütunu verecektir.
Matlab’da Matrisler Üzerinde Değişiklik Yapma
Matlab’da Matrislerin Yeniden Şekillendirilmesi
Matlab’da Bir Matrisin Elemanlarının Bir Vektörün Elemanlarına Atanması
Örnek :
A = [15 2 4 ; 3 7 11 ; 1 2 9];
C = A(:)
C =
15
3
1
2
7
2
4
11
9
Matlab’da Matrislerin Boyutunun Değiştirilmesi
Matlab’da A(m x n) boyutunda bir matris var ise, bu matris m*n = p*q olmak şartıyla B(pxq) boyutunda bir matrise dönüştürülebilir.
Örnek
$latex
A = \begin{bmatrix}
10 & 8 & 6 \\
1 & 3 & 5
\end{bmatrix}
$
A matrisi (2×3) boyutlarınındadır. A matrisini (3X2) boyutuna getiriniz.
Örnek :
A = [10 8 6 ; 1 3 5];
B = reshape(A,3,2)
B =
10 3
1 6
8 5
Matlab’da Matrislerin Genişletilmesi
Matlab’da matrisin bir elemanına atama yapılmışsa , bu matrisi uygun boyutta alması için gereken ama herhangi bir değer ataması yapılmamış elemanlarına otomatik olarak sıfır atanır.
Örnek :
X(3, 1 : 2) = [5 6]
X =
0 0
0 0
5 6
Örnek :
B = [11 10; 9 8];
>> B(2,3)= 5
B =
11 10 0
9 8 5
Matlab’da Bir Matrise Satır veya Sütun Eklenmesi
B = [B x] → satır eklenmesi
B = [B ; y] → sütun eklenmesi
Örnek
$latex
B = \begin{bmatrix}
13 & 6 & 7 \\
14 & 5 & 9 \\
12 & 4 & 11
\end{bmatrix}
$ $latex
x = \begin{bmatrix}
4 \\
5 \\
6
\end{bmatrix}
$ $latex
y = \begin{bmatrix}
15 & 2 & 3
\end{bmatrix}
$
B matrisine x vektörünü ekleyiniz.
B = [13 6 7 ; 14 5 9 ; 12 4 11];
x = [4 ; 5 ; 6];
C = [B x]
C =
13 6 7 4
14 5 9 5
12 4 11 6
B matrisine y vektörünü ekleyiniz.
B = [13 6 7 ; 14 5 9 ; 12 4 11];
y = [15 2 3];
>> D = [B ; y]
D =
13 6 7
14 5 9
12 4 11
15 2 3
Matlab’da Bir Matrisin Satır/Sütununun Silinmesi
Örnek :
$latex
X = \begin{bmatrix}
5 & 11 & 10 \\
4 & 8 & 7 \\
2 & 3 & 9
\end{bmatrix}
$
X matrisinin ilk satır ve sütununu siliniz.
X = [5 11 10 ; 4 8 7 ; 2 3 9];
>> X(1 , :)=[ ]
X =
4 8 7
2 3 9
Bir matrisin içinden tek bir eleman silinemez çünkü matrisin tek bir elemanının silinmesi boyut uyumsuzluğuna sebep olacaktır.
Örnek
$latex
X = \begin{bmatrix}
9 & 13 & 7 \\
11 & 8 & 4 \\
2 & 10 & 3
\end{bmatrix}
$
X = [9 13 7; 11 8 4; 2 10 3];
X(1,2)= []
Subscripted assignment dimension mismatch.
Matlab’da Matrislerin Birleştirilmesi
Örnek
$latex
X = \begin{bmatrix}
2 & 10 \\
5 & 7
\end{bmatrix}
$ $latex
Y = \begin{bmatrix}
11 & 13 \\
4 & 9
\end{bmatrix}
$
matrislerini birleştiriniz.
X = [2 10 ; 5 7];
Y = [11 13 ; 4 9];
W =[X Y]
W =
2 10 11 13
5 7 4 9
Z = [X ; Y]
Z =
2 10
5 7
11 13
4 9
Matris ve Vektörler ile ilgili diğer konular:
Matlab’da Vektör İşlemleri
Matlab’da Vektör Tanımlama, Matlab’da Bir Vektörün Tranzposu, Matlab linspace komutu, Matlab logspace komutu, Matlab mean komutu,Matlab length komutu, Matlab max komutu, Matlab min komutu,Matlab prod komutu,Matlab sign komutu, Matlab find komutu,Matlab fix komutu, Matlab floor komutu
Matlab’da Matrislerin Aritmetik İşlemleri
-
Matlab’da Matrislerin Toplanması
-
Matlab’da Matrislerin Birbirinden Çıkarılması
-
Matlab’da Matrislerin Çarpılması
-
Matlab’da .* işlemi
Matlab’da Özel Matrisler
Sıfır matrisi: Matlab zeros komutu, Birler matris: Matlab ones komutu, Birim matris: Matlab eye komutu, Random matrisi: Matlab rand komutu, Köşegen (diagonal) matris: Matlab diag komutu
Matlab’da Matrisler ile İlgili Özel Komutlar
-
Matlab’da Bir Matrisin Determinantının Alınması: Matlab det komutu
-
Matlab’da Bir Matrisin Rankının Alınması: Matlab rank komutu
-
Matlab’da Bir Matrisin İzinin Bulunması: Matlab trace komutu
-
Matlab’da Bir Matrisin Tersinin Bulunması: Matlab inv komutu
-
Matlab’da Bir Matrisin Karakteristik Denkleminin Bulunması: Matlab poly komutu
-
Matlab’da Bir Matrisin Özdeğer ve Özvektörlerinin Bulunması: Matlab eig komutu
-
Matlab’da Bir Matrisin Ortogonal Matrisinin Bulunması: Matlab orth komutu
-
Matlab’da find komutunun matrislere uygulanışı
-
Matlab’da sort komutunun matrislere uygulanışı
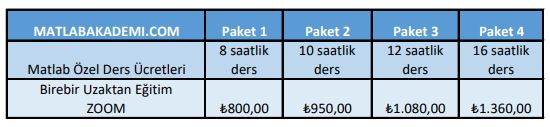
UZAKTAN MATLAB BİREBİR ÖZEL DERS:
Temel Matlab Eğitimi verilmektedir. Eğitim ZOOM platformu üzerinden bire bir uzaktan verilmektedir. Bunun haricinde ödev, proje, tez gibi konularda destek sağlanmamaktadır.
İhtiyaca bağlı olarak ders içeriğinin bazı kısımları daha detaylı ele alınabilmektedir.
Uzaktan eğitim ders taleplerinizi GSM numaranızı da belirterek matlabakademi@gmail.com adresine gönderebilirsiniz.